Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 124

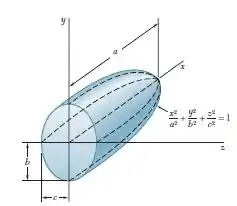
Determine por integração direta o momento de inércia em relação ao eixo z do corpo em formato de semielipsoide mostrado na figura, considerando que ele tem massa específica uniforme e massa m .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A primeira coisa a se fazer é as equações do elispoide em função de y para o plano x y e de z para o plano x z . Temos:

y = b 1 - x 2 a 2

E:

z = c 1 - x 2 a 2

Por definição também vamos precisar do diferencial de massa:

d m = ρ d V

d m = ρ A d x

d m = ρ π y z d x

d m = ρ π b c 1 - x 2 a 2 d x

Integrando, teremos:

m = ∫ 0 a ρ π b c 1 - x 2 a 2 d x

m = ρ π b c x - x 3 3 a 2 0 a

m = 2 3 π ρ a b c

Passo 2

Usaremos a equação do momento de inércia de área da elipse:

I = π 4 z y 3

O momento de inércia geométrico de forma diferencial é dado por:

d I = ρ t I

d I = ρ d x π 4 z y 3

Passo 3

Agora, para calcularmos em relação ao eixo z , vamos utilizar o teorema dos eixos paralelos:

d I z = d I + x 2 d m

Substituindo as equações, temos que:

d I z = 3 m 2 a b 2 4 1 - 2 x 2 a 2 + x 4 a 4 + x 2 - x 4 a 2 d x

I z = ∫ 0 a 3 m 2 a b 2 4 1 - 2 x 2 a 2 + x 4 a 4 + x 2 - x 4 a 2 d x

I z = 3 m 2 a b 2 4 x - 2 x 3 3 a 2 + x 5 5 a 4 + x 3 3 - x 5 5 a 2 0 a

Resolvendo, encontraremos:

I z = 1 5 m a 2 + b 2

Resposta

I z = 1 5 m a 2 + b 2

Ver Outros Exercícios desse livro