Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 6

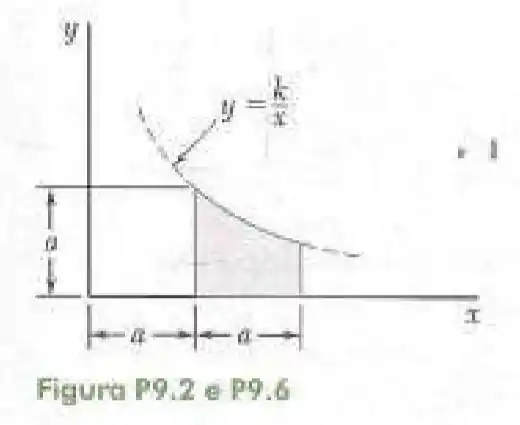
6- Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo x .

Passo 1

Como temos um ponto da parábola em relação a ( a , a ) então o valor de k aplicando esse ponto é:

a = k a → k = a 2

E por mais que nós queiramos a inércia em relação a x nós vamos fazer linhas verticais para encontrarmos o elemento de área. Para fazer por linhas horizontais teria que dividir a superfície em duas dando um trabalho mó desnecessário.

Lembrando que a inércia em x é calculado da seguinte forma:

I x = ∫ y 2   d A

Passo 2

Logo por linhas verticais temos:

d A = y   d x

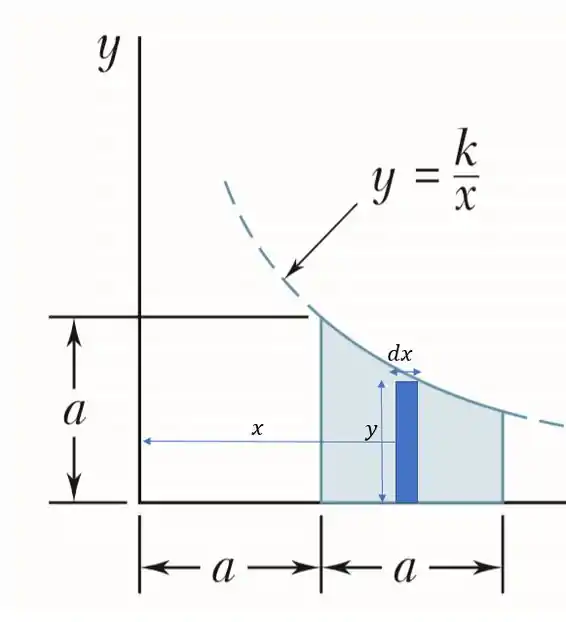
Onde y = a 2 x

Nos dando a seguinte integral para resolver, sabendo que x varia de a até 2 a :

I x = ∫ a 2 a y 3   d x

I x = ∫ a 2 a a 6 x 3   d x

Onde : 1 x 3 = x - 3 , então fazendo a integral:

I x = a 6   x - 2 - 2   a 2 a

Aplicando o intervalo temos:

I x = a 6 1 - 2 × 4 a 2 - - 1 - 2 × a 2

I x = a 6 - 1 8 a 2 + 1 2 a 2

I x = a 4 4 - 1 8 = 3 a 4 8

Passo 3

Ué mais um passo? Não acabou? Pois é amiguinho é aqui que a vida te prega uma peça e você erra questão não sabendo por onde, os elementos verticais tem distâncias de x diferentes em relação a origem logo temos que considerar um fator de 1 / 3 , por conta de sua área.

d I x = 1 3   y 2   d A

Então:

I x = 1 3 3 a 4 8 = a 4 8

Resposta

I x = a 4 8

Ver Outros Exercícios desse livro