Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas de Revisão - Ex. 4

Determine o momento de inércia de área em relação ao eixo x . Depois, usando o teorema dos eixos paralelos, determine o momento de inércia em relação ao eixo x ' que passa pelo centroide C da área. y - = 120   m m .

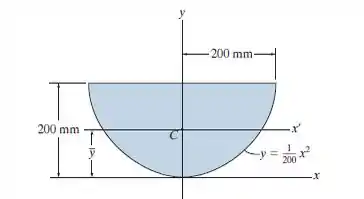
Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Esta é uma questão bem direta! Precisamos determinar duas informações. A primeira é o momento de inércia da área em relação ao eixo x . Depois, com posse desse valor, devemos utilizar o teorema dos eixos paralelos pra determinar o momento de inércia em relação ao eixo x ' , que passa pelo centroide C da área.

Então, vamos começar determinando o momento de inércia em relação a x . Por definição, temos:

I x = ∫ A y 2 d A

Então, basta resolvermos esta integral!

Temos aqui uma região do tipo I, cujos limites de integração são - 200 ≤ x ≤ 200 e x 2 200 ≤ y ≤ 200 .

Fazendo esta substituição, chegamos a seguinte integral:

I x = ∫ - 200 200 ∫ x 2 200 200 y 2 d y d x

Então, vamos as contas!

Passo 2

Agora nosso trabalho é braçal. Precisamos desenvolver a integral do Passo 1. Portanto,

I x = ∫ - 200 200 ∫ x 2 200 200 y 2 d y d x

I x = ∫ - 200 200 y 3 3 x 2 200 200 d x

I x = ∫ - 200 200 200 3 3 - x 6 200 3 ⋅ 3 d x

I x = 200 3 x 3 - x 7 200 3 ⋅ 7 ⋅ 3 - 200 200

I x = 2 ⋅ 200 4 3 - 200 7 200 3 ⋅ 7 ⋅ 3

I x = 914 ⋅ 10 6   m m 4

Passo 3

E para finalizarmos a questão, temos que utilizar o teorema dos eixos paralelos. Ele nos diz que:

I = I G + A d 2

Sendo I G o momento de inércia que passa pelo centro de massa da peça, I o momento de inércia que queremos e d a distância entre os dois eixos.

Como nós ainda não temos a área, vamos calculá-la. Portanto,

A = ∫ A d A ∫ - 200 200 ∫ x 2 200 200 d y d x

A = ∫ - 200 200 y x 2 200 200 d x

A = ∫ - 200 200 200 - x 2 200 d x

A = 200 x - x 3 200 ⋅ 3 - 200 200

A = 2 ⋅ 200 2 - 200 3 200 ⋅ 3 = 53,33 ⋅ 10 3   m m 2

Sendo assim, como a distância de x até x ' é y - = 120   m m , temos:

I x = I x ' + A y - 2

914 ⋅ 10 6 = I x ' + 53,33 ⋅ 10 3 ⋅ 120 2

I x ' = 146 ⋅ 10 6   m m 4

E assim finalizamos a questão!

Resposta

I x = 914 ⋅ 10 6   m m 4

I x ' = 146 ⋅ 10 6   m m 4

Ver Outros Exercícios desse livro