Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 73

Determine a orientação dos eixos principais, que têm sua origem no ponto C , e os momentos de inércia principais da seção transversal em relação a esses eixos.

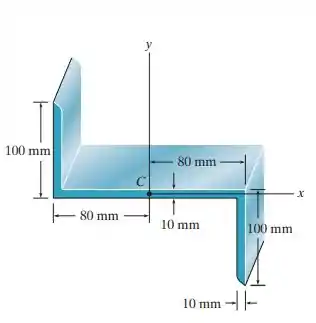
Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Primeiramente, vamos determinar os momentos de inércia em cada eixo:

I y = 1 12 10 140 3 + 2 1 12 10 0 10 3 + 10 0 10 75 2 = 13,533 × 10 6   m m 4

I x = 1 12 140 10 3 + 2 1 12 10 100 3 + 10 100 45 2 = 5,7283 × 10 6   m m 4

Sabemos que:

I x y = ∑ I x ' y ' + A d x d y = 0 + 0 + 10 100 - 75 45 + 0 + 10 100 75 - 45 I x y = - 6,75 × 10 6   m m 4

Passo 2

Sabemos que o momento principal de inercia é dado por:

I m i n m á x = I x + I y 2 ± I x + I y 2 + I x y 2

Substituindo:

I m í n = 17,44 × 10 6   m m 4 I m á x = 1 , 8 4 × 10 6   m m 4  

Passo 3

A orientação dos eixos principais, com origem em C vai ser:

tan ⁡ 2 θ p = - I x y I x - I y 2 θ p = 60,04 °

Substituindo o valor de θ p na equação de I u , temos:

I u = I x + I y 2 + I x - I y 2 cos ⁡ 2 θ - I x y sin ⁡ 2 θ I u = 17,44 × 10 6   m m 4

Logo:

θ 1 = 60 ° θ 2 = - 3 0 °

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

I m í n = 17,44 × 10 6   m m 4 I m á x = 1,84 × 10 6   m m 4

θ 1 = 60 ° θ 2 = - 30 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de inércia da área da seção transversal em relação ao eixo x .
Determine a distância x - até o centroide C da área da seção transversal da viga; depois, ache o momento de inércia I - y ' em relação ao eixo y ' .
Determine y - , que localiza o eixo centroidal x ' da área da seção transversal da viga “ T ” , e depois calcule o momento de inércia em relação ao eixo x ' .
Determine a distância y - até o centroide C da área da seção transversal da viga; depois, ache o momento de inércia I - x em relação ao eixo x ' .
Determine o produto de inércia do área sombreada em relação aos eixos x e y .