Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 111

Determine o momento de inércia de área da seção transversal da viga em relação ao eixo x que passa pelo centro C .

Passo 1

O problema pede que encontremos o momento de inércia no eixo x .

Primeiro, começaremos dividindo a figura em triângulos e quadrados e calculando algumas distâncias, assim:

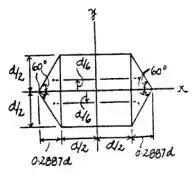
Passo 2

Então, vamos no final do livro pegar os momento de inércia do triângulo e do quadrado:

I x t r i a n = 1 36 b h 3

I x q u a d = 1 1 2 b ( h 3 )

Passo 3

Agora, vamos calcular o momento de inercia com as informações que temos, em relação ao eixo x , fica:

I x = ∑ I y + A d x 2

Então:

I x = 1 1 2 d d 3 + 0 + 4 1 36 0,2887 d d 2 3 + 1 2 0,2887 d d 2 d 6 2

Calculando isso, chegamos á:

I x = 0,95 d 4

Resposta

I x = 0,95 d 4

Ver Outros Exercícios desse livro