Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 116
Determine o momento de inércia de área da seção transversal da viga em relação aos eixos e tendo sua origem localizada no centroide . Suponha que todos os cantos sejam ângulos retos.
Passo 1
O problema pede que encontremos o momento de inércia no eixo e , que tem origem no centroide .
Primeiro, vamos calcular as distâncias dos centroides de cada elemento, assim:
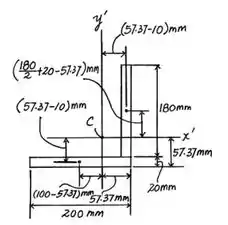
Passo 2
Então basta encontrar o momento de inércia, nós podemos encontrar a formula do momento de inércia de cada elemento no final livro, então fica: