Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 111

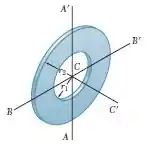
Determine o momento de inércia de massa do anel de massa m , cortado de uma placa delgada uniforme, com relação a ao eixo A A ' b ao eixo centroidal C C ' que é perpendicular ao plano do anel.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos que a área do anel é dada por:

A = π r 2 2 - r 1 2

Também sabemos que a área pode ser dada por:

A = m ρ t

Onde t é a espessura do anel e ρ a densidade. Portanto:

π r 2 2 - r 1 2 = m ρ t

ρ t = m π r 2 2 - r 1 2

Passo 2

Logo, o momento de inércia em massa sobre o eixo centroidal é dado por:

I A A ' = ρ t I A A ' á r e a

I A A ' = m π r 2 2 - r 1 2 π 4 r 2 4 - r 1 4

I A A ' = m 4 r 2 2 - r 1 2 r 2 2 + r 1 2 r 2 2 - r 1 2

I A A ' = m 4 r 2 2 + r 1 2

Passo 3

O momento de inércia de massa do eixo C C ' é dado por:

I C C ' = I A A ' + I B B '

Logo:

I C C ' = m 4 r 2 2 + r 1 2 + m 4 r 2 2 + r 1 2

I C C ' = m 2 r 2 2 + r 1 2

Resposta

a )   I A A ' = m 4 r 2 2 + r 1 2

b )   I C C ' = m 2 r 2 2 + r 1 2

Ver Outros Exercícios desse livro