Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 106

Para uma dada superfície, os momentos de inércia em relação a dois eixos retangulares centroidais x e y são I x = 468 × 10 6   m m 4 e I y = 117 × 10 6   m m 4 , respectivamente. Sabendo que após a rotação dos eixos x e y de 30 ° no sentido anti-horário em torno do centroide o produto de inércia relativo aos eixos girados é 566 × 10 6   m m 4 , use o círculo de Mohr para determinar a a orientação dos eixos principais, b os momentos de inércia centroidais principais.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos calcular o momento médio de inércia:

I m é d = 1 2 I x + I y

I m é d = 1 2 468 + 117 × 10 6

I m é d = 292,5 × 10 6   m m 4

O círculo de Mohr será:

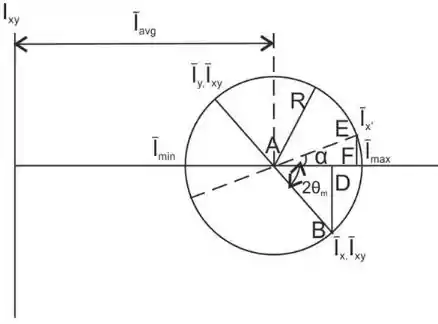
Passo 2

Agora vamos calcular a orientação dos eixos principais a partir do círculo de Mohr.

2 θ m + α = 60 °

A análise geométrica de A B D nos permite admitir que:

R = I x - I m é d cos ⁡ 2 θ m

R = 468 - 292,5 cos ⁡ 2 θ m × 10 6

R = 175,5 cos ⁡ 2 θ m × 10 6

A análise geométrica de A E F nos permite admitir que:

R = I x ' - I m é d cos ⁡ α

R = 566 - 292,5 cos ⁡ α × 10 6

R = 273,5 cos ⁡ α × 10 6

Como:

2 θ m + α = 60 °

Temos que:

α = 60 - 2 θ m

Passo 3

Vamos equacionar R :

273,5 cos ⁡ α = 175,5 cos ⁡ 2 θ m

Como:

2 θ m + α = 60 °

Temos que:

α = 60 ° - 2 θ m

Logo:

273,5 cos ⁡ 60 ° - 2 θ m = 175,5 cos ⁡ 2 θ m

175,5 cos ⁡ 60 ° cos ⁡ 2 θ m + sen ⁡ 60 ° sen ⁡ 2 θ m = 273,5 cos ⁡ 2 θ m

175,5 1 2 cos ⁡ 2 θ m + 3 2 sen ⁡ 2 θ m = 273,5 cos ⁡ 2 θ m

87,75 cos ⁡ 2 θ m + 151,99 sen ⁡ 2 θ m = 273,5 cos ⁡ 2 θ m

tan ⁡ 2 θ m = 185,75 151,99

tan ⁡ 2 θ m = 1,222

Logo:

2 θ m = 50,71

E:

θ m = 25,35 °

Passo 4

Agora podemos calcular o valor de R :

R = 175,5 cos ⁡ 2 θ m × 10 6

R = 277,133 × 10 6   m m 4

Portanto, os momentos principais máximos e mínimos serão:

I m á x , m í n = I m é d ± R

I m á x , m í n = 292,5 × 10 6 ± 277,133 × 10 6

Logo:

I m á x = 596,633 × 10 6   m m 4

I m í n = 15,367 × 10 6   m m 4

Resposta

a )   θ m = 25,35 °

b )   I m á x = 596,633 × 10 6   m m 4

I m í n = 15,367 × 10 6   m m 4

Ver Outros Exercícios desse livro