Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 145

Determine o momento de inércia de massa do objeto de aço mostrado na figura em relação (a) ao eixo x (b) ao eixo y (c) ao eixo z (A massa específica do aço é ).

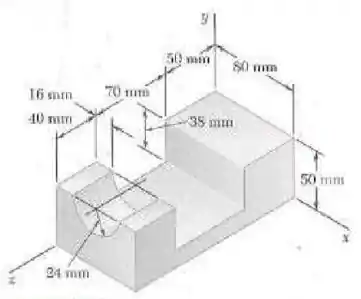
Passo 1

Primeiro, vamos pegar o numero de massa de cada elemento! Vamos considerar como elemento 1 todo o paralelepípedo solido (sem contar os espaços tirados), e os elementos 2 e 3 são os buracos que faltam dentro da peça, que são respectivamente, o buraco no meio da peça e o semi circulo na ponta da peça! Então, vamos lá! Primeiramente, vamos calcular a massa pela formula da densidade:

Logo,

Passo 2

Agora que temos as massas, vamos aplicar o teorema dos eixos pararelos, para achar os momentos de inercia de massa de cada elemento e soma-los! A figura 9.28 pode auxiliar você para calcular o momento de inercia de massa para os elementos 1 e 2. E as equações derivadas dela te ajudam para calcular o elemento 3!

Passo 3

Vamos fazer o mesmo para o momento no eixo .

Passo 4