Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 97

Determine o momento de inércia de massa I z do sólido formado girando-se a área sombreada em torno do eixo z . A densidade do material é ρ = 7,85   M g / m 3 .

Passo 1

O problema pede que encontremos o momento de inércia no eixo y .

Primeiro, vamos pensar sobre a massa:

m = ρ ⋅ V

De forma derivada fica:

d m = ρ ⋅ d V = ρ π r 2 d y

Passo 2

Agora sim vamos para o momento de inércia no eixo z , para isso a gente sabe que de forma derivada temos:

d I z = 1 2 d m ( r ) 2

Ou seja:

d I z = 1 2 ρ π r 2   d z r 2 = 1 2 ρ π r 4 d z = 1 2 ρ π z 2 8 4 d z

Simplificando isso, chegamos á:

d I z = ρ π 8192 z 8   d z

Calculamos então, o momento de inércia pela integral:

I z = ∫ d I z = ∫ 0 4 ρ π 8192 z 8   d z

Resolvendo, a gente encontra:

I z = 32 9 ⋅ ρ π

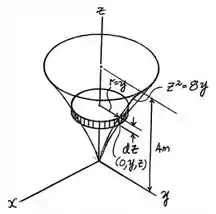
Passo 3

Está quase acabando, agora gente substitui a densidade ρ e calcula o resultado:

I z = 32 9 ⋅ ρ π

I z = 32 9 ⋅ ( 7,85 ⋅ 10 3 ) π

I z = 87,7 ⋅ 10 3   k g ⋅ m 2

Resposta

I z = 87,7 ⋅ 10 3   k g ⋅ m 2

Ver Outros Exercícios desse livro