Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 48
Determine o momento de inércia polar da área mostrada na figura em relação ao ponto , ao centroide da superfície.
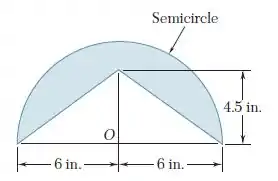
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A estrutura foi dividida conforme a figura a seguir:
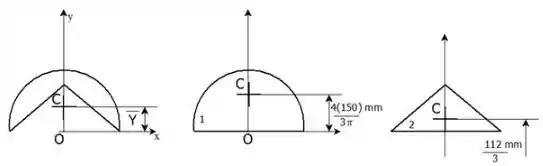
A forma pode ser obtida subtraindo de .
Passo 2
O momento polar da zona com relação a é dado por:
Portanto:
Resolvendo, encontraremos:
Passo 3
O item nos pede o momento polar com relação ao centroide da superfície. Temos que:
Portanto:
Precisamos então descobrir :
Construindo a seguinte tabela, temos que:
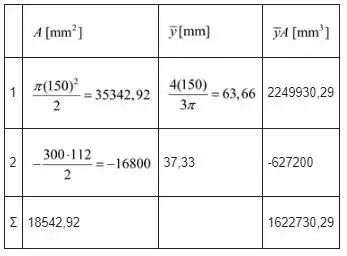
Portanto:
Logo:
Passo 4
Agora é só substituir os valores: