Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 7

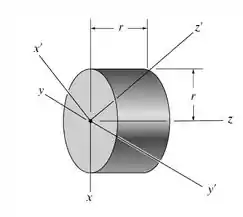
Determine os momentos de inércia para o cilindro homogêneo de massa m em relação aos eixos x’, y’ , z’.

Passo 1

Devido a simetria pode-se fazer as seguintes considerações:

I x y = I y z = I z x = 0

E que os momentos de inércia I x , I y e I z serão:

I y = I x = 1 12 m 3 r 2 + r 2 + m r 2 2 = 7 m r 2 12

I z = 1 2 m r 2

Passo 2

Para o eixo x’, temos que os vetores unitários são:

u x = cos ⁡ 135 ° = - 1 2

u y = cos ⁡ 90 ° = 0

u z = cos ⁡ 135 ° = - 1 2

Dessa forma o momento de inércia I x ' será:

I x ' = I x ( u x ) 2 + I y ( u y ) 2 + I z ( u z ) 2 - 2 I x y u x u y - 2 I y z u y u z - 2 I z x u z u x

I x ' = 7 m r 2 12 - 1 2 2 + 0 + 1 2 m r 2 - 1 2 2 - 0 - 0 - 0

I x ' = 13 m r 2 24

Passo 3

Para o eixo y’ o momento de inércia I y ' será:

I y ' = I y = 7 m r 2 12

Passo 4

Para o eixo z’, temos que os vetores unitários são:

u x = cos ⁡ 135 ° = - 1 2

u y = cos ⁡ 90 ° = 0

u z = cos ⁡ 45 ° = 1 2

Dessa forma o momento de inércia I Z ' será:

I z ' = I x ( u x ) 2 + I y ( u y ) 2 + I z ( u z ) 2 - 2 I x y u x u y - 2 I y z u y u z - 2 I z x u z u x

I z ' = 7 m r 2 12 - 1 2 2 + 0 + 1 2 m r 2 1 2 2 - 0 - 0 - 0

I z ' = 13 m r 2 24

Resposta

De acorco com os passos 1,2,3 e 4 os momentos de inércia para o cilindro homogêneo de massa m em relação aos eixos x’, y’ , z’ são respectivamente:

I x ' = 13 m r 2 24

I y ' = 7 m r 2 12

I z ' = 13 m r 2 24

Ver Outros Exercícios desse livro