Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 196

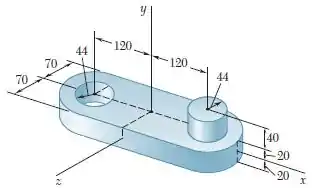
Determine os momentos de inércia e os raios de giração do elemento de máquina de aço mostrado na figura em relação aos eixos x e y . (A massa específica do aço é 7.850   k g / m 3 )

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos o seguinte diagrama:

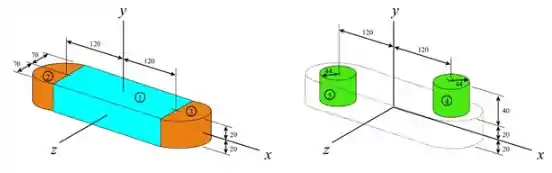
Sabemos que m = ρ V .

m 1 = 7850   k g / m 3 0,28   m ( 0,04   m ) 0,14   m

m 1 = 10,5504   k g

Temos também que:

m 2 = m 3 = 7850   k g / m 3 π 2 0,07 2 0,04  

m 2 = m 3 = 2,41683   k g

E:

m 4 = m 5 = 7850   k g / m 3 0,04   m π 0 , 0 4 4   m 2

m 4 = m 5 = 1,90979   k g

Passo 2

O momento de inércia de massa em relação ao eixo x é dado por:

I x = I x 1 + I x 2 + I x 3 + I x 4 - I x 5

Logo:

I x 1 = 10,5504 12 40 2 + 140 2

I x 1 = 18639   k g ⋅ m m 2

I x 2 = I x 3 = 2,41683 70 2 4 + 40 2 12

I x 2 = I x 3 = 3282,9   k g ⋅ m m 2

I x 4 = 1,90979 44 2 4 + 40 2 12 + 20 + 40 2 2

I x 4 = 4234,6   k g ⋅ m m 2

I x 5 = 1,90979 44 2 4 + 40 2 12

I x 5 = 1179   k g ⋅ m m 2

Portanto:

I x = 18639   k g ⋅ m m 2 + 2 3282,9   k g ⋅ m m 2 + 4234,6   k g ⋅ m m 2 - 1179   k g ⋅ m m 2

I x = 28,3 × 10 - 3   k g ⋅ m 2

Passo 3

O momento de inércia de massa em relação ao eixo y é dado por:

I y = I y 1 + I y 2 + I y 3 + I y 4 - I y 5

Logo:

I y 1 = 10,5504 12 240 2 + 140 2

I y 1 = 6 7874   k g ⋅ m m 2

I y 2 = I y 3 = 2,41683 70 2 1 2 - 16 9 π 2 + 120 + 4 70 3 π

I y 2 = I y 3 = 57956   k g ⋅ m m 2

I y 4 = 1,90979 1 2 44 2 + 120 2

I y 4 = 29350   k g ⋅ m m 2

I y 5 = 1,90979 44 2 4 + 40 2 12

I y 5 = 29350   k g ⋅ m m 2

Portanto:

I y = 67874   k g ⋅ m m 2 + 2 57956   k g ⋅ m m 2 + 29350   k g ⋅ m m 2 - 29350   k g ⋅ m m 2

I y = 183,8 × 10 - 3   k g ⋅ m 2

Passo 4

Para calcular o raio de giração precisamos saber qual a massa total. Temos que:

m = m 1 + m 2 + m 3 + m 4 - m 5

m = m 1 + 2 m 2

m = 10,5504 + 2 2,41683

m = 15,38406   k g

Logo:

k x = I x m

k x = 28,3 × 10 - 3 15,38406

k x = 42,9   m m

E:

k y = I y m

k y = 183,8 × 10 - 3 15,38406

k y = 109,3   m m

Resposta

I x = 28,3 × 10 - 3   k g ⋅ m 2

I y = 183,8 × 10 - 3   k g ⋅ m 2

k x = 42,9   m m

k y = 109,3   m m

Ver Outros Exercícios desse livro