Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 69
Determine o produto de inércia para a área parabólica em relação aos eixos e .
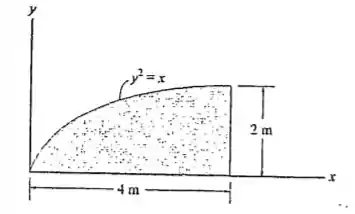
Passo 1
Nosso diferencial de produto de inércia como a função não está “encaixada” nos eixos certinhos será dado por
Integrando ambos os lados vamos ter