Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 73

Se o pino B é liso, determine as componentes da reação no pino A e no apoio fixo C.

Passo 1

Vamos começar desenhando o diagrama do corpo livre (DLC) do primeiro elemento:

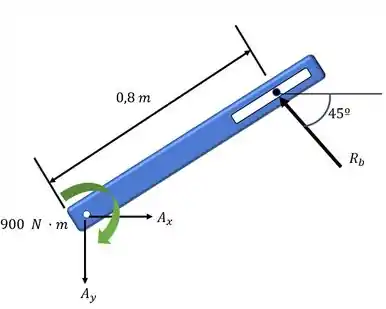
A força Rb causa momento no sentido anti-horário e o momento (em verde) já dado é de 900 Nm no sentido horário. Vamos usar a equação do equilíbrio para o momento no ponto A:

Σ M A = 0 R b × 0,8 - 900 = 0 ⇒ R b = 900 0,8 R b = 1125   N   ( 1 )

Passo 2

Podem-se aplicar as equações do equilíbrio para o mesmo elemento:

Σ F x = 0 A x - R b × cos ⁡ 45 º = 0   ( 2 )

Substituindo 1 em ( 2 ) :

A x - 1125 × cos ⁡ 45 º = 0   A x = 795,49 ≈ 795   N

Passo 3

Σ F y = 0 - A y + R b × sin ⁡ 45 º = 0   ( 3 )

Substituindo 1 em ( 3 ) :

- A y + 1125 × sin ⁡ 45 º = 0 A y = 795,49 ≈ 795   N

Passo 4

Agora desenhamos o diagrama do corpo livre (DLC) para o segundo elemento

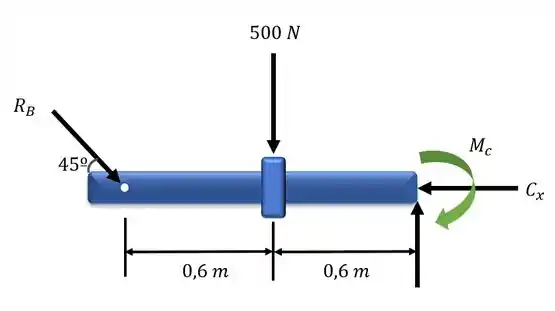
Podemos começar utilizando a equação do equilíbrio para o momento em relação ao ponto C.

A força Rb e a força de 500 N causam momento anti-horário em relação ao ponto C, ao passo que o momento Mc é dado e está no sentido horário. Podemos escrever a equação do equilíbrio em relação ao momento para o ponto C:

Σ M C = 0 R b × sin ⁡ 45 º × 1,2 + 500 × 0,6 - M c = 0   4

Substituindo 1 em 4 :

1125 × sin ⁡ 45 º × 1,2 + 500 × 0,6 - M c = 0 1254,6 - M c = 0 M c = 1,25 × 10 3   N ⋅ m M c = 1,25   k N ⋅ m

Passo 5

Aplicando a equação do equilíbrio para o elemento no eixo x:

Σ F x = 0 - C x + R b × cos ⁡ 45 º = 0   ( 5 )

Substituindo ( 1 ) em 6 :

- C x + 1125 × cos ⁡ 45 º = 0   ( 5 )

C x = 795   N

Aplicando a equação do equilíbrio para o elemento no eixo y:

Σ F y = 0 C y - R b × cos ⁡ 45 º - 500 = 0   ( 6 )

Substituindo ( 1 ) em ( 6 ) :

C y - 1125 × cos ⁡ 45 º - 500 = 0  

C y = 1295,49 ≈ 1295   N

C y = 1295   N = 1,30   k N

Resposta

A x = 795   N

A y = 795   N

C x = 795   N

C y =   1,30   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tubo de esgoto de 1,4 Mg é mantido nas pinças da empilhadeira. Determine as forças normais em A e B como funções do ângulo da lamina θ e represente graficamente os resultados de força(eixo vertical)
Um diagrama esquelético de uma mao segurando uma carga é mostrado na figura abaixo. Se a carga e o antebraço possuem massas de 2 kg e 1,2 kg, respectivamente e seus centros de massa estão localizados
Quando os freios de um avião são acionados, a roda do nariz exerce duas forças sobre a extremidade do trem de pouso, como mostra a figura .Determine as componentes horizontal e vertical da reação no p
Determine a reação normal no rolete A e as componentes horizontal e vertical no pino B para o equilíbrio
Se o rolete B pode sustentar uma carga máxima de 3 kN, determine a maior intensidade de cada uma das três forças F que podem ser sustentadas pela estrutura.