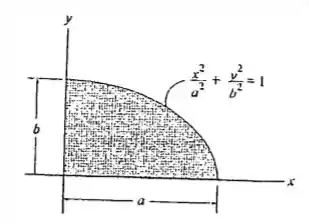
Determine o produto de inércia de um quarto de área elíptica em relação aos eixos e .

O elemento diferencial de área paralelo ao eixo é dado por . Além disso, temos que

As coordenadas do centroide para essa figura são dadas por

Sendo assim, o diferencial do produto inercial com relação aos eixos será

Então, nosso produto inercial será dado pela integração de ambos os lados, assim