Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 107

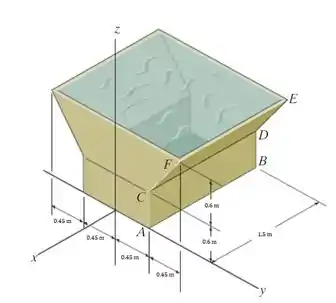
O tanque é usado para armazenar um líquido com um peso específico de 10   k N / m ³ . Se o tanque estiver cheio, determine a intensidade da força hidrostática sobre as placas C D E F e A B D C .

Passo 1

Nesse tanque, as paredes C D E F e A B D C têm larguras fixas, o que nos leva a poder representar o carregamento por conta da pressão do fluido como uma distribuição em 2D, conforme a figura abaixo.

A barragem tem 8 metros de largura, beleza? Tendo isso em mente, vamos descobrir a intensidade de carga que a água causa na barragem:

w F = γ h F b

w C = γ h C b

w A = γ h A b

w F = 1000 0 1,5 = 0   N / m

w C = 1000 0,6 1,5 = 900   N / m

w A = 1000 1,2 1,5 = 1800   N / m

Passo 2

A força resultante da água na barragem pode ser escrita através do produto da intensidade de carga da água pelo comprimento da barragem. Para a parede C D E F precimosa encontrar esse valor! O desenho abaixo mostra a situação:

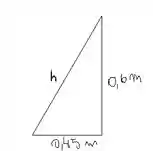
Pelo teorema de Pitágoras, temos:

h 2 = 0,45 2 + 0,6 2

h 2 = 0,5625

h = 0,75   m

Desse modo, as forças que atuam nas paredes são iguais a:

F C D E F = 1 2 ( w F + w C ) b

F C D E F = 1 2 0 + 900 0,75

F C D E F = 337,5   N

Na outra parede:

F A B D C = 1 2 w C + w A b

F A B D C = 1 2 900 + 1800 0,6

F A B D C = 810   N

Resposta

A intensidade da força hidrostática sobre as placas C D E F e A B D C é:

F C D E F = 337,5   N

F A B D C = 810   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barragem de um lago é projetada para suportar a força adicional causada pelo lodo depositado no fundo do lago. Admitindo que o lodo é equivalente a um liquido de densidade ρ s = 1,76 ⋅ 10 3k g / m 3
A base da barragem de um lago é projetada para resistir a até 120 % da força horizontal da água. Após a construção verificou-se a disposição de lodo (que é equivalente a um líquido de densidade ρ s =
Determine a força única equivalente e a distância do ponto A até sua linha de ação para a viga e a carga do ( a ) Problema 3.101b, ( b ) Problema 3.101d, ( c ) Problema 3.101e.
107- Uma viga suporta três cargas com intensidade indicada na figura e uma quarta carga cuja intensidade é função da posição. Se b = 1.5m e as cargas forem representadas por uma única força equivalent
O carregamento sobre a prateleira da estante está distribuído como mostra a figura. Determine a posição da resultante equivalente, medida a partir do ponto O.