Iaii, pessoal? Essa questão é bem compridinha, então vamo lá, sem estresse!

1. Usando relações trigonométricas:

Primeiro vamos analisar as equações que nos foram dadas:

Aplicando as relações temos que essas duas equações são equivalentes a, respectivamente:

Uma vez que , nós temos que, colocando em evidência:

Considerando que , nós temos que:

Dessa relação, nós podemos concluir que:

Sabendo disso, já podemos encontrar o valor de , utilizando a trigonometria:

Sendo que, o ângulo entre será:

Passo 2

2. Usando adição de vetor:

Adotando um valor arbitrário para , os movimentos harmônicos de se comportam como mostrado na figura abaixo:



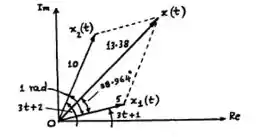
Para adição de vetores, encontramos que:

Passo 3

3. Usando números complexos:

Para nós temos as seguintes partes reais:

Considerando que , nós temos que:

Desenvolvendo, temos que:

Dessa forma, encontramos que:

Com isso, temos as ferramentas suficientes pra concluir que: