Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 53

53- Duas cantoneiras de L 76 × 76 × 6.4   m m são soldadas a um perfil C de 250 × 30 . Determine os momentos de inércia da seção composta em relação aos eixos centroidais paralelo e perpendicular a junção do perfil C .

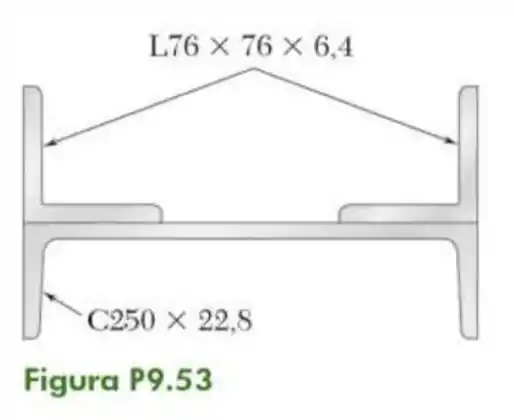
Passo 1

Os dados das cantoneiras são:

I x = 0.512 × 10 6   m m 4

I y = 0.512 × 10 6   m m 4

A = 929   m m 2

x ¯ = y ¯ = 21.2   m m

Esse último dado nos diz que x e y diferem do centro de gravidade em 21.2 m m da seguinte forma:

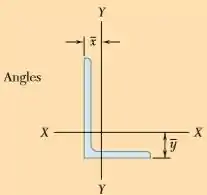
E a do perfil em C será:

A = 2890   m m 2

I x = 28 × 10 6   m m 4

I y = 0.945 × 10 6   m m 4

y ¯ = - 16.1   m m

e i x o   m a i o r = 254   m m

Onde o perfil em C terão as inércias trocadas pois esse perfil estaria na vertical (o eixo maior pelo menos estando em y ) e essa está na horizontal, como pode se ver na figura abaixo.

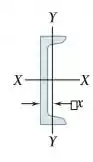
E a posição em y do centro de posição desse perfil ficará na negativa pois ele está virado para baixo.

Isso nos dá uma posição vertical do centroide igual a (a posição horizontal ficará no meio da estrutura mesmo, por conta da simetria horzontal):

y ¯ = 2890 × - 16.1 + 2 × 929 × 21.2 2890 + 2 × 929 = - 1.5037   m m

Passo 2

Calculando a inércia em y dos corpos nós temos:

I y - c a n t o n e i r a s = 2 × 0.512 × 10 6 + 929 × 254 2 - 21.2 2 = 21.82 × 10 6

I y - p e r f i l = I x = 28 × 10 6   m m 4

Isso nos dá uma inércia total de:

I y = I y - c a n t o n e i r a s + I y - p e r f i l = 49.82 × 10 6 m m 4

Passo 3

Agora a inércia em x :

I x - c a n t o n e i r a s = 2 × 0.512 × 10 6 + 929 × 21.2 2 = 1.86 × 10 6   m m 4

I x - p e r f i l = 0.945 × 10 6 + 2890 × 16.1 2 = 1.69 × 10 6 m m 4

Logo a inércia em x   do corpo será:

I x = I x - c a n t o n e i r a s + I x - p e r f i l = 3.55 × 10 6   m m 4

Resposta

I y = 49.82 × 10 6 m m 4

I x = 3.55 × 10 6   m m 4

Ver Outros Exercícios desse livro