Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 32

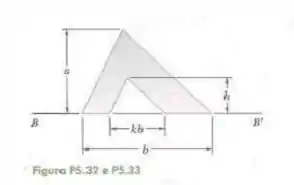
Determine a distância h para a qual o centroide da área sombreada fique o mais distante de BB’, quando (a) k = 0,1   e   b k = 0,8 .

Passo 1

Fala aí galera, vamos pra mais um problema de estática. Vamos primeiro calcular o centroide em termos dos elementos fornecidos. Logo:

A × y - t r i â n g u l o   m a i o r = a 3 × a b 2 = a 2 b 6

A × y - t r i â n g u l o   m e n o r = h 3 × k h b 2 = k b h ² 6

Logo, o centroide será:

y - = a 2 b - k b h 2 6 a b - k h b 2 = a 2 b - k b h 2 3 a b - k h b

Para achar o máximo valor do centroide, basta derivar em relação a h   e igualar a 0:

d y - d h = - 2 k b h ( 3 a b - k h b ) - - 3 k b ( a 2 b - k b h 2 ) 3 a b - k h b 2 = 0

- 2 k b h 3 a b - k h b - - 3 k b a 2 b - k b h 2 = 0

3 k b h 2 - 6 a b h + 3 a 2 b = 0

Chegamos a uma equação de segundo grau, logo:

∆ = 36 a 2 b 2 - 36 a ² b ² k

h = 6 a b ± 6 a b 1 - k 6 k b

h = a ± a 1 - k k

Passo 2

Agora, basta substituir os valores dados para acharmos os valores em cada letra.

Na letra a, k = 0,1 :

h 1 = 0,513 a

h 2 = 19,48 a

O segundo valor não faz sentido, pois é maior que a.

Na letra b, temos que k = 0,8 :

h 1 ' = 1,8 a

h 2 ' = 0,691 a

O Primeiro resultado não faz sentido, pois é maior que a.

Resposta

  1. h = 0,513 a
  2. h = 0,691 a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide x - da área.
Localize o centroide x - do setor circular.
Localize o centroide y - da área.
Localize o centroide x - da área sombreada.
Localize o centroide y - da área.