Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 6.Problemas - Ex. 33

No edifício de quatro andares mostrado na Figura 6.30, não há nenhuma rotação da seção horizontal no nível dos pisos. Considerando-se que os pisos são rígidos e que a massa total está concentrada nos níveis dos pisos, deduza as equações de movimento do edifício utilizando:

  1. a segunda lei do movimento de Newton;
  2. equações de Lagrange.

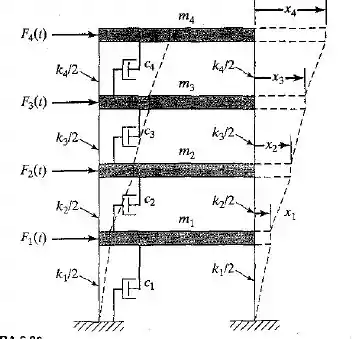
Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?

Primeiro, vamos ilustrar a forma a cadeia de cisalhamento da forma seguinte:

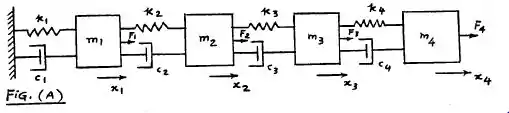
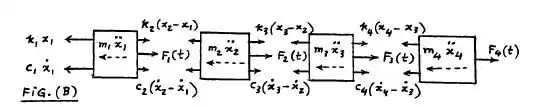
Dessa forma, trataremos da letra (a), fazendo as equações de movimento, de acordo com o corpo livre mostrado na última ilustração:

  1. segunda lei do movimento de Newton

    2. m 1 x ¨ 1 + c 1 x ˙ 1 + k 1   x 1 - c 2 x ˙ 2 - x ˙ 1 - k 2 x 2 - x 1 = F 1 ( t )

    m 2 x ¨ 2 + c 2 x ˙ 2 - x ˙ 1 + k 2 x 2 - x 1 - c 3 x ˙ 3 - x ˙ 2 - k 3 x 3 - x 2 = F 2 ( t )

    m 3 x ¨ 3 + c 3 x ˙ 3 - x ˙ 2 + k 3 x 3 - x 2 - c 4 x ˙ 4 - x ˙ 3 - k 4 x 4 - x 3 = F 3 t

    m 4 x ¨ 4 + c 4 x ˙ 4 - x ˙ 3 + k 4 x 4 - x 3 = F 4 ( t )

    Passo 2

  2. equações de Lagrange

Inicialmente, temos por definição que essas equações são:

d d t δ T δ q ˙ j - δ T δ q j + δ V δ q j + δ D δ q ˙ j = Q j

Onde T representa a energia cinética, V representa a energia potencial, R representa a função de dissipação de Rayleigh, Q j = j t k representa força generalizada e q j = j t k representa a coordenada generalizada. Logo, temos que:

T = 1 2 ( m 1 x ˙ 1 2 + m 2 x ˙ 2 2 + m 3 x ˙ 3 2 + m 4 x ˙ 4 2 )

V = 1 2 ( k 1 x 1 2 + k 2 x 2 - x 1 2 + k 3 x 3 - x 2 2 + k 4 x 4 - x 3 2 )

R = 1 2 ( c 1 x ˙ 1 2 + c 2 x ˙ 2 - x ˙ 1 2 + c 3 x ˙ 3 - x ˙ 2 2 + c 4 x ˙ 4 - x ˙ 3 2 )

Q j = F j ;         j = 1,2 , 3,4

q j = x j ; j = 1,2 , 3,4

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro