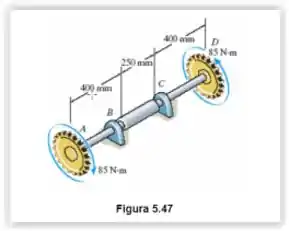
O eixo de aço A-36 é composto pelos tubos e e uma seção maciça . Está apoiado em mancais lisos que permitem que ele gire livremente. Se as engrenagens, presas às extremidades do eixo, forem submetidas a torques de , determine o ângulo de torção da extremidade da seção maciça em relação à extremidade . Os tubos têm diâmetro externo de e diâmetro interno de . A seção maciça tem diâmetro de .

Olá, pessoal! Tudo bem com vocês?

O nosso problema pede que determinemos o ângulo de torção da extremidade da seção maciça em relação à extremidade e nos fornece os seguintes dados sobre a seção .

Aço A-36, portanto,

Primeiramente fazemos o diagrama de corpo livre:

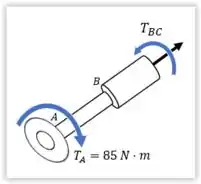
Cortando uma seção através do eixo :

Para encontrar o ângulo de torção, utilizaremos a fómula:

O momento polar de inércia, , é dado por:

Substituindo na fórmula do ângulo de torção, temos: