O eixo é constituído de uma barra que tem uma massa por unidade de comprimento de . Determine as componentes da reação nos mancais e se, no instante mostrado, o eixo gira livremente e tem uma velocidade angular . Qual é a aceleração angular do eixo nesse instente? O mancal pode suportar um componente de força na direção , enquanto o mancal não pode.
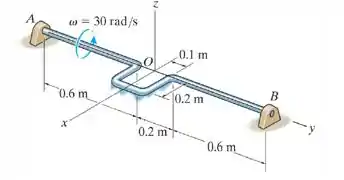
Passo 1
O DCL do problema é mostrado abaixo.
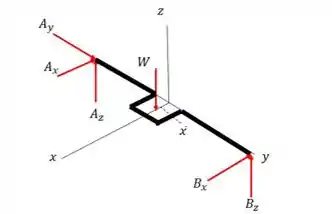
O peso do sistema é determinado por
A posição do centro de massa será
O momento de inércia de massa em e serão
Passo 2
Sabendo que
Assim, aplicando a equação do movimento em relação a direção , temos
Eq. 1:
Para direção
Da mesma forma, para a direção :
Eq. 2:
Passo 3
Fazendo o somatório das forças nas três direções, temos
Eq. 3:
Assim,
E
Eq. 4:
Resolvendo o sistema formado pelas equações (2) e (3), obtemos
Similarmente, resolvendo (1) e (4), encontramos
Resposta
Os componentes das reações são: , e . E a aceleração angular do eixo é igual a .