Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 80
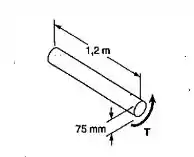
O eixo sólido mostrado é de um aço doce o qual se considera elastoplástico com G=77GPa e τ=145MPa. Determinar o ângulo de torção causado pela aplicação de um torque T1 = 9 kN.m e T2 = 14,7 kN.m.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos o eixo e dizermos qual deveria ser o maior torque para que ele não tivesse uma tensão maior do que aquela. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser determinar a razão dos raios e a tensão..
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
Resposta
Exercícios de Livros Relacionados
Enquanto o eixo de aço de seção transversal mostrado rotaciona 120r p m , uma medida estroboscópica indica que o ângulo de giro é de 2 ° em um comprimento de 4m . Utilizando G = 77.2G P a , determine
Determine a tensão de cisalhamento máxima em um eixo de seção transversal cheia de 38m m de diâmetro, quando ele transmite 75h p a uma velocidade de (a) 750r p m e (b) 1500r p m .
Utilizando uma tensão de cisalhamento admissível 31M P a , projete um eixo de seção transversal cheia, feito de aço para transmitir 12h p na velocidade de (a) 1200r p m e (b) 2400r p m .
Os dois eixos de seção cheia e as engrenagens mostrados são utilizados para transmitir 16 hp do motor A operando a uma rotação de 1260 rpm, para uma máquina ferramenta em D. Sabendo que a tensão de ci
450 r p m. Sabendo que r = 12m m , determine determine a potência máxima que pode ser transmitida sem exceder a tensão de cisalhamento admissível de 51.7M P a .