Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 68
Enquanto o eixo de aço de seção transversal mostrado rotaciona , uma medida estroboscópica indica que o ângulo de giro é de em um comprimento de . Utilizando , determine a potência transmitida.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a potência transmitida, então vejam a seção que iremos utilizar :D
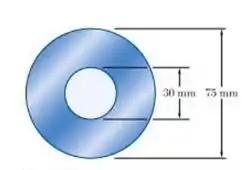
Considere os seguintes dados fornecidos no exercício:
Então podemos encontrar J:
Sabendo que podemos determinar o torque a partir da equação do ângulo :D
Isolando o torque temos:
Passo 2
Sabendo que a frequência é de:
Podemos calcular a potência 0/
Resposta
.
Exercícios de Livros Relacionados
Um torque T aplicado a uma barra maciça feita de um material elastoplástico é aumentado até que a barra se torne completamente plástica, e então é removida:Mostrar que a distribuição de tensões residu
Determinar o maior torque T que pode ser aplicado a cada uma das duas barras de alumínio mostradas, e o correspondente ângulo de torção em B, sabendo – se que τ a d m = 50M P a e G = 26G P a .
Determinar o maior torque T que pode ser aplicado a cada uma das duas barras de latão mostradas, e o correspondente ângulo de torção em B, sabendo – se que τ a d m = 8 0M P a e G = 39G P a .
Cada uma das duas barras de latão mostradas está sujeita a um torque de intensidade T = 1,4k N m . Sabendo-se que G = 39 G P a , determinar para cada barra a máxima tensão de cisalhamento e o ângulo d
Cada uma das barras de alumínio mostradas está sujeita a um torque de intensidade T = 1800N m . Sabendo-se que G = 26 G P a , determinar para cada barra a máxima tensão de cisalhamento e o ângulo de t