Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 1.Problemas - Ex. 8

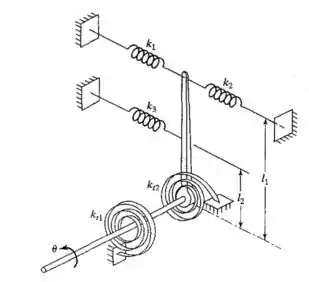
Na Figura 1.60, determine a constante elástica equivalente do sistema na direção de θ .

Passo 1

Caaalma, sem pânico. A questão parece um monstro, mas vou mostrar pra vocês que tá tudo tranquilo. Primeiro vamos somar na nossa constante equivalente as molas radiais. A formula a força elástica pra elas é:

1 2 k θ 2

Passo 2

Pra gente relacionar com as molas que não são radiais, mas estão relacionadas com o movimento a uma distancia l do eixo, temos:

1 2 k θ l 2

E tudo isso se relaciona na equivalência com:

1 2 k e q θ 2

Passo 3

Agora vamos juntar tudo! Temos que:

1 2 k e q θ 2 = 1 2 k t 1 θ 2 + 1 2 k t 2   θ 2 + 1 2 k 1 θ l 1 2 + 1 2 k 2 θ l 1 2 + 1 2 k 3 θ l 2 2

Agora vem a parte da álgebra! Vamos tirar o θ 2 da equação. Logo:

k e q = k t 1 + k t 2 + k 1 l 1 2 + k 2 l 1 2 + k 3 l 2 2

Resposta

k e q = k t 1 + k t 2 + k 1 l 1 2 + k 2 l 1 2 + k 3 l 2 2

Ver Outros Exercícios desse livro