11- A força que atua no dente da engrenagem é . Decomponha a força nos componentes que atuam ao longo das linhas e .
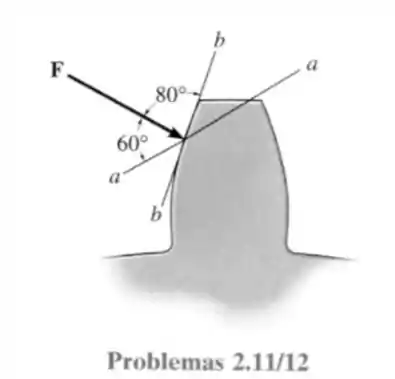
Passo 1
Vamos considerar que as forças nas linhas e estão entrando no ponto de cruzamento entre as linhas e com isso traçar nossa estratégia para resolver a questão.
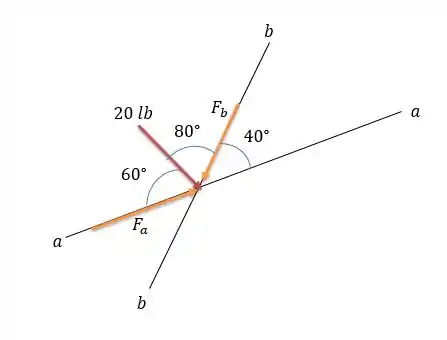
Passo 2
Dessa forma até podemos tratar o eixo como horizontal e um eixo normal a ela como a vertical mas isso nos daria um trabalho um tanto quanto desnecessário. Com isso sabemos que as forças e são originárias da força de sendo essa última força a resultante dessas outras duas. Então podemos transportar a força de modo a formar o seguinte triângulo de forças.
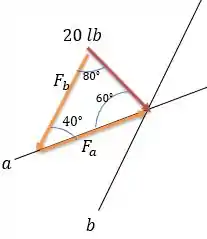
Pela lei dos senos podemos encontrar.
E também: