4.8. Determine a intensidade, a direção e o sentido do momento resultante das forças em em relação ao ponto O.
Passo 1
Vamos começar esquematizando o problema.
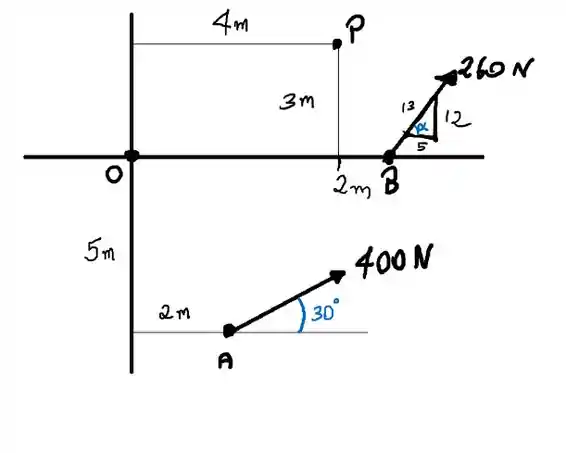
O momento resultante é a soma dos momentos.
Então
Passo 2
Vamos começar calculando

E
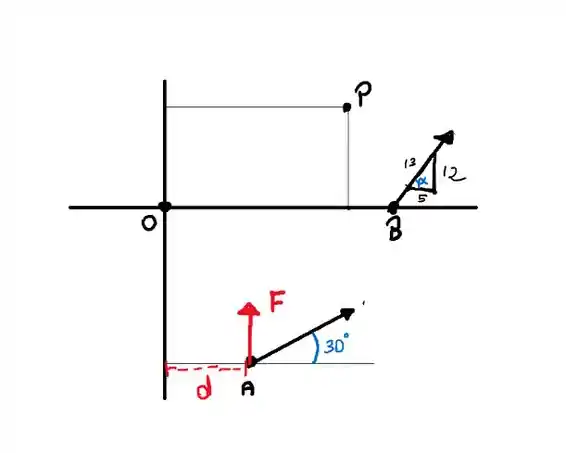
Então
Passo 3
Agora
Repare que o ponto O e a força B estão na mesma linha horizontal, por tanto a distância é 0.
E

Pelo triângulo
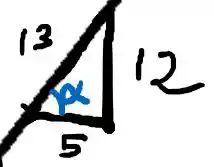
Então
Então
Passo 4
Agora podemos determinar
Resposta
Seu sentido é anti-horário.