Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 75

Localize o centroide x -   da área da seção transversal da viga e depois os momentos de inércia e o produto de inércia dessa área em relação aos eixos u e v. Os eixos têm sua origem no centroide C.

Passo 1

Passo 2

Escrevendo em uma tabela o tamanho de cada segmento do respectivo centro de massa:

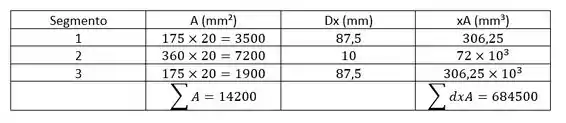
Passo 3

Sabemos que:

x - = ∑ d x A ∑ A x - = 684500 14200 = 48,2   m m

Passo 4

Escrevendo em uma tabela os valores de momento de inércia em relação ao eixo x numa tabela:

Passo 5

Podemos calcular o momento de inércia da peça I x como: I x = I x - + A d 2 I x = 77,99 × 10 6 + 252,7 × 10 6 I x = 330,69 × 10 6   m m 4

Passo 6

Escrevendo em uma tabela os valores de momento de inércia em relação ao eixo y numa tabela:

Passo 7

Podemos calcular o momento de inércia da peça I y como: I y = I y - + A d 2 I y = 18,1 × 10 6 + 21,318 × 10 6 I y = 39,418 × 10 6   m m 4

*Devido à simetria, I x y = 0

Passo 8

O momento de inércia em relação ao eixo u pode ser calculado como:

I u = I x + I y 2 + I x - I y 2 c o s 2 θ - I x y s e n 2 θ θ = - 60 º

Portanto:

I u = 330,69 × 10 6 + 39,418 × 10 6 2 + 330,69 × 10 6 - 39,418 × 10 6 2 × cos ⁡ 2 ⋅ - 60 - 0 × s e n 2 θ I u = 112,236 × 10 6   m m 4

Passo 9

O momento de inércia em relação ao eixo v pode ser calculado como:

I v = I x + I y 2 - I x - I y 2 c o s 2 θ + I x y s e n 2 θ θ = - 60 º

Portanto:

I v = 330,69 × 10 6 + 39,418 × 10 6 2 - 330,69 × 10 6 - 39,418 × 10 6 2 × cos ⁡ 2 ⋅ - 60 + 0 × s e n 2 θ I v = 257,872 × 10 6   m m 4

Passo 10

O momento de inércia em relação a uv pode ser calculado como:

I u v = I x - I y 2 s e n 2 θ + I x y c o s 2 θ θ = - 60 º

Portanto:

I u v = 330,69 × 10 6 - 39,418 × 10 6 2 × s e n   2 - 60 - 0 × c o s 2 θ I u v = - 126,124 × 10 6   m m 4

Resposta

I u = 112,236 × 10 6   m m 4

I v = 257,872 × 10 6   m m 4

I u v = - 126,124 × 10 6   m m 4

Ver Outros Exercícios desse livro