Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 122
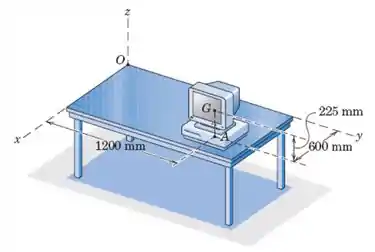
A massa do computador é de com o centro de massa no ponto . Determine o momento do peso correspondente em relação ao ponto sobre a mesa. Encontre o módulo de
Passo 1
E aí meus queridxs, tudo bem com vocês?
Se liguem só que essa questão é um pouco mais chatinha e exige um pouco de atenção, mas nada que a gente não seja capaz de fazer. Se liguem só, antes de tudo vamos escrever o ponto em função dos nossos eixos, então, dado que o ponto é
Escrevendo de forma vetorial vamos ter
Além disso, temos que o peso do nosso computador vai ser dado por
Passo 2
Com isso, vamos calcular o momento em relação a cada um dos eixos lembrando que a direção na qual o momento vai surgir é dado pela regra da mão direita. Assim, teremos
Em não vamos ter tendência de rotação, então, . Então temos
Com isso, para encontrar o módulo faremos
Pronto, tá resolvido nosso problema.
