Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 131

A barra dobrada tem uma massa  ρ  por unidade de comprimento. Determine o momento do peso de barra em relação ao ponto  O .

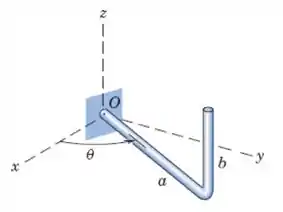
Passo 1

Note que teremos duas forças que causam momento em torno de O uma da barra de comprimento a e a outra de comprimento b (iremos trabalhar com elas separadas somente por motivos de comodidade mesmo). Além disso, separaremos o peso de cada barra, concentrando-o na metade da barra de comprimento a e um outro peso na extremidade da barra. Como a massa da nossa barra é dada por m = ρ ⋅ d (densidade vezes comprimento) e, portanto, seu peso será dado por

m g = ρ g d

Lembrando mais uma vez que vai estar atuando no ponto médio de cada barra.

Passo 2

Sendo assim, calculando o momento (a direção será dada com a regra da mão direita) com relação ao eixo x vamos ter

M x = ρ g b ⋅ cos ⁡ θ ⋅ a ⋅ j ^ + ρ g a ⋅ a 2 ⋅ cos ⁡ θ   j ^

Analogamente para o eixo y temos

M y = - ρ g b ⋅ s e n θ ⋅ a ⋅ i ^ - ρ g a ⋅ a 2 ⋅ sen ⁡ θ   i ^

Nosso momento devido ao peso será dado por

M = M x + M y = ρ g b ⋅ cos ⁡ θ ⋅ a ⋅ j ^ + ρ g a ⋅ a 2 ⋅ cos ⁡ θ   j ^ - ρ g b ⋅ s e n θ ⋅ a ⋅ i ^ - ρ g a ⋅ a 2 ⋅ sen ⁡ θ   i ^

M = ρ g a ⋅ b ⋅ cos ⁡ θ j ^ + a 2 ⋅ cos ⁡ θ j ^ - b ⋅ sen ⁡ θ i ^ - a 2 ⋅ s en ⁡ θ i ^

M = ρ g a ⋅ b + a 2 ⋅ cos ⁡ θ j ^ - sen ⁡ θ i ^

Pronto, tá resolvido nosso problema.

Resposta

M = ρ g a ⋅ b + a 2 ⋅ cos ⁡ θ j ^ - sen ⁡ θ i ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas cargas ascendentes são exercidas na pequena treliça tridimensional. Reduza essas duas cargas a um único sistema de força-binário no ponto O. Mostre que R → é perpendicular a M O → . Em seguida, d
Ao apertar um parafuso cujo centro está no ponto O, a pessoa exerce uma força de 40l b na alavanca da catraca com a mão direita. Além disso, com a mão esquerda, ele exerce uma força de 20l b , conform
A espaçonave de Prob. 2/135 está repetida aqui. O plano é disparar quatro propulsores de 1,2l b conforme mostrado a fim de girar a espaçonave em torno de seu eixo z , mas o propulsor em A falha. Deter
Substitua as duas forças e um binário agindo na estrutura do tubo rígido por sua força resultante equivalente R → agindo no ponto O e um binário M O → .
Substitua as duas forças que atuam no sólido retangular por um torçor. Escreva o momento M → associado ao torçor como um vetor e especifique as coordenadas do ponto P no plano x - y através do qual pa