22- A máxima força de tração permissível em um elemento de treliça é e a máxima força de compressão permissível é . Determine as intensidades máximas das duas cargas que podem ser aplicadas a treliça. Suponha que e .
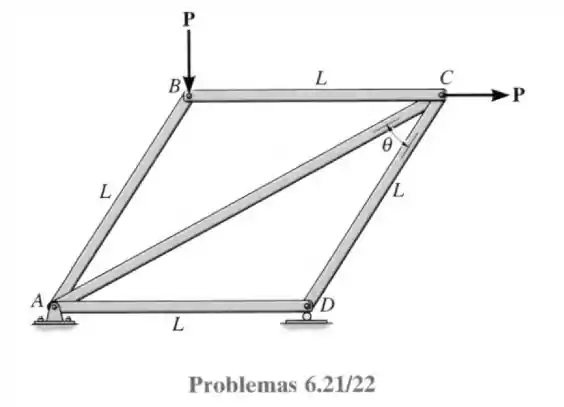
Passo 1
Pela questão passada temos as seguintes forças nas barras:
Se substituirmos o valor de temos:
Passo 2
Com isso temos que a maior força de compressão será a que tem a menor constante, logo:
E a maior força de tração será:
Substituindo então o maior valor que pode se ter para tração e compressão temos:
E para tração:
Se passarmos de a barra arrebenta por tração então devemos utilizar ela, pois é o menor valor.