- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão. Considere que e .
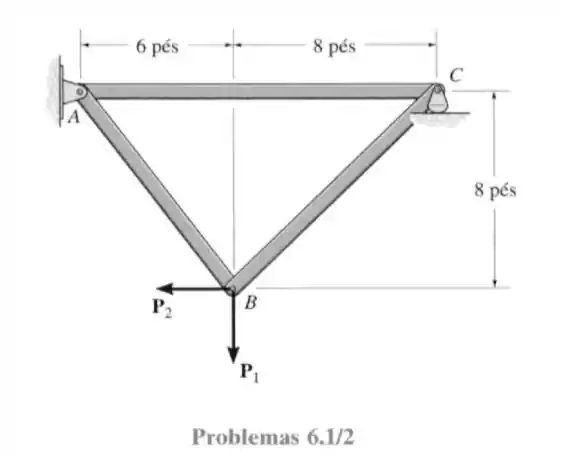
Passo 1
Como a próxima questão é parecida com essa, vamos fazer pelo método das juntas nessa questão e calculando pela força de reação nos apoios na próxima.
E para resolver esse exercício pelo método das juntas, vamos considerar que todas as forças saem do nó , se as forças ou forem positivas, teremos uma força trativa, caso seja negativa será compressiva.

Onde e valem:
Onde precisamos do ângulo para saber a força na barra por .
Passo 2
Fazendo a somatória das forças em no nó temos:
E fazendo a somatória das forças em no ponto teremos:
Isso nos dará o seguinte sistema:
Isso nos dá:
Por ser positiva é uma força de tração.
E a outra força será:
Também será uma força trativa.
Passo 3
Para a somatória das forças no nó temos que saber as reações no nó , como a única força horizontal ativa é de e a única força de reação horizontal encontra-se em logo teremos o seguinte sistema de forças:
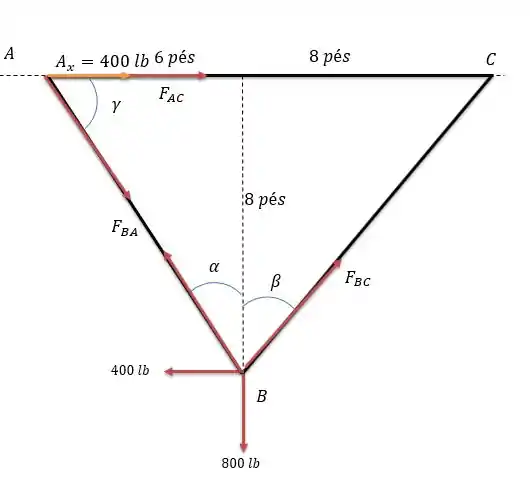
Fazendo a somatória das forças :
O que caracteriza uma força compressiva, pois o resultado deu negativo.