Organize o problema de autovalor do Exemplo 6.10 em termos das coordenadas q 1 = x 1 ,q 2 = x 2 , q 3 = x 3 - x 2 e resolva o problema resultante. Compare os resultados obtidos com os do Exemplo 6.10 e tire conclusões.

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 6.Problemas - Ex. 44

Organize o problema de autovalor do Exemplo 6.10 em termos das coordenadas e resolva o problema resultante. Compare os resultados obtidos com os do Exemplo 6.10 e tire conclusões.

Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?

Inicialmente, vamos escrever as equações de movimento pro sistema mostrado no enunciado. São as seguintes:

Agora, como expresso no enunciado, vamos repetir essas equações, porém substituindo que . Teremos:

E então, dividiremos cada equação pela massa correspondente. Vamos ter que:

Passo 2

Dito isso, vamos manipular essas equações afim de obter nosso objetivo. Primeiro, faremos a subtração de (E.1) – (E.2):

A subtração de (E.2) – (E.3) nos dá:

Agora a equação (E.1), (E.4) e (E.5), respectivamente, podem ser expressas da seguinte forma, substituindo as incógnitas que nos foram dadas no enunciado:

Em seguida, vamos pegar esse sistema de equações e fazer que . Isso vai nos dar:

Por último, vamos fazer a forma matricial dessas equações onde . Teremos:

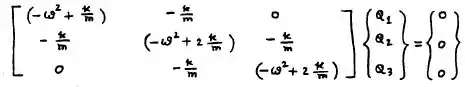
Passo 3

Para tanto, nós teremos as equações de frequência assim:

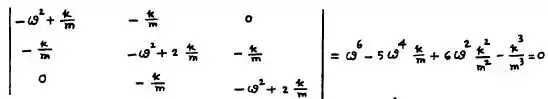
Disso, nós tiramos que:

As raízes dessa equação resultam em:

A conclusão é que os autovalores são os mesmos em ambos os problemas.

Resposta