Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 80
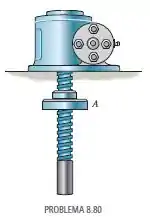
O parafuso de rosca quadrada tem um diâmetro médio de 20 mm e um avanço de rosca de 4 mm. Se a massa da placa A é 2 kg, determine o menor coeficiente de atrito estático entre o parafuso e a placa para que ela não desça pelo parafuso quando for suspensa conforme mostra a figura.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Sabemos que o ângulo de fricção é dado por:
Portanto:
O ângulo de avanço do parafuso é dado por:
Substituindo os dados, temos que:
Passo 2
Agora vamos calcular o menor torque necessário para afrouxar o parafuso. Temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
Determine a menor força aplicada P necessária para mover o calço A para a direita. A mola está comprimida por uma distância de 175 mm. Desconsidere os pesos de A e de B. O coeficiente de atrito es
Determine a força de retenção sobre a placa A se o parafuso for apertado com um torque de M = 8N ⋅ m . O parafuso de rosca quadrada tem raio médio de 10m m e avanço de rosca de 3m m , e o coeficiente
Se a força F for removida do cabo do macaco no Problema 8.65 , determine se o parafuso é autotravante.
O parafuso de rosca quadrada é usado para unir duas placas. Se o parafuso tem diâmetro médio d=20m m e avanço de rosca l=3 m m , determine o menor torque M necessário para afrouxar o parafuso se a tra