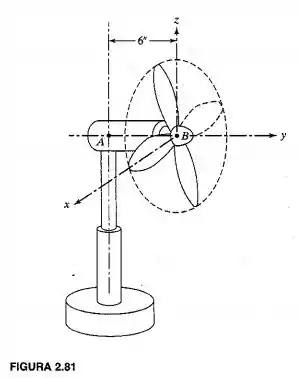
Uma das pás de um ventilador elétrico é removida (como mos tram as linhas tracejadas na Figura 2.81). O eixo de aço AB, no qual as pás estão montadas, é equivalente a um eixo uniforme de 1 in de diâmetro e 6 in de comprimento. Cada pá pode ser modelada como uma haste delgada uniforme de 2 lb de peso e 12 in de comprimento. Determine a frequência natural de vibração das três pás restantes em relação ao eixo y.

Oi, tudo bem?

Queremos a frequencia de vibração natural do sistema. Ela é dada por:

Vamos calcular o momento polar de inércia do eixo sobre a sua transversal:

Substituindo os dados, temos que:

Agora vamos calcular a rigidez torcional. Temos que:

Substituindo os dados, temos que:

Como já temos , precisamos calcular o momento de inércia de massa do sistema. Temos que:

Substituindo os dados, temos que:

Agora é só calcular a frequencia natural de torção: