Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 2.Problemas - Ex. 71

Determine a equação de movimento da barra rígida uniforme O A de comprimento l e massa m mostrada na Figura 2.86 . Determine também sua frequência natural.

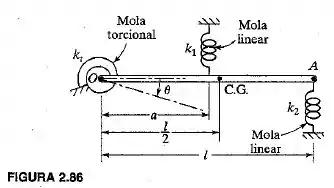
Passo 1

Queremos a frequência natural do sistema dado na figura do enunciado.

Vamos calcular o momento de inércia de massa do sistema:

J O = 1 12 m l 2 + m l 2 2

J O = 1 3 m l 2

A equação de movimento para o sistema fornecido é da forma:

J O θ ¨ = - k 1 θ - k 1 a θ a - k 2 l θ l

1 3 m l 2 θ ¨ = - k 1 θ - k 1 a θ a - k 2 l θ l

1 3 m l 2 θ ¨ + k 1 + k 1 a 2 + k 2 l 2 θ = 0

A equação generalizada de movimento para o sistema é da forma:

θ ¨ + ω n 2 θ = 0

Portanto:

θ ¨ + k 1 + k 1 a 2 + k 2 l 2 1 3 m l 2 θ = 0

θ ¨ + 3 k 1 + k 1 a 2 + k 2 l 2 m l 2 θ = 0

A frequência natural será:

ω n 2 = 3 k 1 + k 1 a 2 + k 2 l 2 m l 2

ω n = 3 k 1 + k 1 a 2 + k 2 l 2 m l 2

Resposta

1 3 m l 2 θ ¨ + k 1 + k 1 a 2 + k 2 l 2 θ = 0

ω n = 3 k 1 + k 1 a 2 + k 2 l 2 m l 2

Ver Outros Exercícios desse livro