Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 195

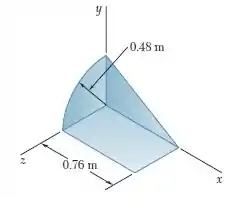
Um pedaço de chapa metálica de 2   m m de espessura é cortado e dobrado para formar o componente de máquina mostrado na figura. Sabendo que a massa específica do aço é 7850   k g / m 3 , determine o momento de inércia de massa do componente em relação a cada um dos eixos coordenados.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Primeiro, vamos calcular as massas do componente dividido, onde 1 é o retângulo, 2 o triângulo e 3 o quarto de circulo.

Sabemos que m = ρ V .

m 1 = 7850   k g / m 3 2 × 10 - 3   m 0,76   m 0,48   m

m 1 = 5,727   k g

Temos também que:

m 2 = 7850   k g / m 3 2 × 10 - 3   m 1 2 0,76   m 0,48   m

m 2 = 2,863   k g

E:

m 3 = 7850   k g / m 3 2 × 10 - 3   m π 4 0,48   m 2

m 3 = 2,841   k g

Passo 2

O momento de inércia de massa em relação ao eixo x é dado por:

I x = I x 1 + I x 2 + I x 3

Logo:

I x 1 = 5,727 1 12 0,48 2 + 0,48 2 2

I x 1 = 0,44   k g ⋅ m 2

I x 2 = 2,863 1 18 0,48 2 + 0,48 3 2

I x 2 = 0,110   k g ⋅ m 2

I x 3 = 2,841 1 2 0,48 2

I x 3 = 0,327   k g ⋅ m 2

Portanto:

I x = 0,44   k g ⋅ m 2 + 0,110   k g ⋅ m 2 + 0,327   k g ⋅ m 2

I x = 0,877   k g ⋅ m 2

Passo 3

O momento de inércia de massa em relação ao eixo y é dado por:

I y = I y 1 + I y 2 + I y 3

Logo:

I y 1 = 5,727 1 12 0 , 76 2 + 0,48 2

I y 1 = 1,542   k g ⋅ m 2

I y 2 = 2,863 1 18 0,76 2 + 0 , 76 3 2

I y 2 = 0 , 276   k g ⋅ m 2

I y 3 = 2,841 1 4 0,48 2

I y 3 = 0 , 164   k g ⋅ m 2

Portanto:

I y = 1,542   k g ⋅ m 2 + 0,276   k g ⋅ m 2 + 0,164   k g ⋅ m 2

I y = 1,982   k g ⋅ m 2

Passo 4

O momento de inércia de massa em relação ao eixo z é dado por:

I z = I z 1 + I z 2 + I z 3

Logo:

I z 1 = 5,727 1 12 0 , 76 2 + 0 , 76 2 2

I z 1 = 1,103   k g ⋅ m 2

I z 2 = 2,863 1 18 0 , 76 2 + 0,48 2 + 0,76 3 2 + 0 , 48 3 2

I z 2 = 0,385   k g ⋅ m 2

I z 3 = 2,841 1 4 0,48 2

I z 3 = 0 , 164   k g ⋅ m 2

Portanto:

I z = 1,103   k g ⋅ m 2 + 0,385   k g ⋅ m 2 + 0,164   k g ⋅ m 2

I z = 1,652   k g ⋅ m 2

Resposta

I x = 0,877   k g ⋅ m 2

I y = 1,982   k g ⋅ m 2

I z = 1,652   k g ⋅ m 2

Ver Outros Exercícios desse livro