Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 120

O pêndulo consiste em uma barra esbelta O A , que tem uma massa por unidade de comprimento de 3   k g / m . O disco fino tem uma massa por unidade de área de 12   k g / m 2 . Determine a distância y - até o centro de massa G do pêndulo; depois, calcule o momento de inércia do pêndulo em relação a um eixo perpendicular à página e passando por G .

Passo 1

O problema pede que encontremos o centroide y - e calculemos o momento de inércia em relação a um eixo perpendicular à página e que passa por G .

Vamos, calcular logo o centroide em y - :

y - = ∑ y - A ∑ A

y - = 0,75 1,5 3 + 1,8 π 0,3 2 12 - 1,8 [ π 0,1 2 ( 12 ) ] 1,5 3 + π 0,3 2 12 - π 0,1 2 ( 12 )

y - = 1,1713   m

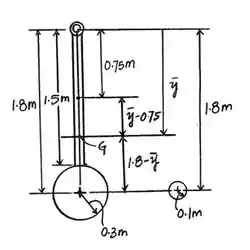
Passo 2

Vamos olhar logo no final do livro as formulas dos momentos de inércia da barra e do disco:

I G 1 = 1 12 m 1 l 2

I G 2 = 1 2 m 2 r 2

I G 3 = 1 2 m 3 r 2

Passo 3

Agora, vamos calcular o momento de inercia com as informações que temos, em relação ao eixo que passa por G , fica:

I G = ∑ I G + m d 2

I G = 1 12 1,5 3 + 1,5 3 1,1713 - 0,75 2 + 1 2 π 0,3 2 12 0,3 2 + π 0,3 2 12 1,8 - 1,1713 2 - 1 2 π 0,1 2 12 0,1 2 - π 0,1 2 12 1,8 - 1,1713 2

Calculando isso, chegamos á:

I G = 2,99   k g ⋅ m 2

Resposta

y - = 1,1713   m

I G = 2,99   k g ⋅ m 2

Ver Outros Exercícios desse livro