Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 22.Problemas - Ex. 16

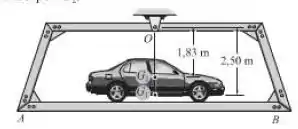
A plataforma A B , quando vazia, tem uma massa de 400   k g , centro de massa em G 1 e período natural de oscilação τ 1 = 2,38   s . Se um carro tendo uma massa de 1,2   M g e centro de massa em G 2 , é colocado na plataforma, o período natural de oscilação torna-se τ 2 = 3,16   s . Determine o momento de inércia do carro em torno de um eixo passando por G 2 .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Considerando o sentido anti horário positivo, temos:

∑ M O = I O α

- m g l sin ⁡ θ = I O θ ¨

Podemos considerar sin ⁡ θ = θ para pequenos deslocamentos, portanto:

θ ¨ + m g l I O θ = 0

Temos que:

p = m g l I O

Como f = p / 2 π , temos:

f = m g l I O 2 π

Queremos o período que é definido como τ = 1 / f . Logo:

τ = 2 π m g l I O

τ = 2 π I O m g l

Aplicando os dados do enunciado, temos:

2,38 = 2 π I O p 400 ( 9,81 ) ( 2,5 )

I O p = 1407,55   k g ⋅ m 2

Para o carro na plataforma, temos que:

l = 2,50 400 + 1,83 ( 1200 ) 1200 + 400

l = 1,9975   m

I O = I O c + I O p

3,16 = 2 π I O c + I O p 160 0 ( 9,81 ) ( 1,9975 )

I O c = 6522,76   k g ⋅ m 2

Portanto:

I G C = I O c - m c d 2

I G C = 6522,76 - 1200 1,83 2

I G C = 2,5 10 3 k g ⋅ m 2

Resposta

I G C = 2,5 10 3 k g ⋅ m 2

Ver Outros Exercícios desse livro