Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 22.Problemas - Ex. 14

O disco, tendo uma massa de 7,5   k g , está preso com pino no seu centro O e suporta o bloco A , que tem uma massa de 1,5   k g . Se a correia que passa sobre o disco não desliza na sua superfície de contato, determine o período natural de vibração do sistema.

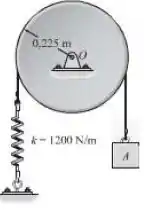
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Considerando o sentido anti horário positivo, temos:

∑ M O = I O α + m a ( 0,225 )

a = 0,225 θ ¨

Resolvendo:

- 1,5 9,81 0,225 - 1200 θ 0,225 0,225 + 1,5 ( 9,81 ) 0,225 = I O θ ¨ + ( 1,5 ) 0,225 2 θ ¨

Temos que:

I O = 1 2 7,5 0,225 2

I O = 0,038

Portanto:

- 3,31 - 60,75 θ + 3,31 = 0,038 θ ¨ + 0,076 θ ¨

θ ¨ + 60,75 0,114 θ = 0

θ ¨ + 532,9 θ = 0

Temos que:

p = 532,9

p = 23,085

Como f = p / 2 π , temos:

f = 23,085 2 π

Queremos o período que é definido como τ = 1 / f . Logo:

τ = 2 π 23,085

τ = 0,2722   s

Resposta

τ = 0,2722   s

Ver Outros Exercícios desse livro