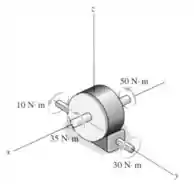
O redutor de velocidade está sujeito a quatro momentos binários. Determine a intensidade do momento de binário resultante e seus ângulos diretores coordenados.
Passo 1
Pela figura podemos ver que temos dois momentos agindo no eixo e outros dois agindo no eixo . Nos dois casos, ambos os momentos favorecem a rotação no sentido anti-horário, que vamos adotar como o sentido positivo:
Cada um desses momentos corresponde a um vetor que aponta na direção dos eixos. Então o momento resultante é dado pelo seguinte vetor:
Portanto:
Passo 2
Os ângulos diretores coordenados de um vetor são os ângulos que ele forma com os eixos. Nesse caso, estamos calculando esses ângulos para o nosso vetor de momento resultante:
Para calcular esses ângulos, vamos lembrar da definição do produto escalar:
Então, se fizermos o produto escalar do vetor com os vetores , e , vamos encontrar so ângulos que ele forma com cada um dos eixos.
Se é o ângulo entre é o eixo :
E podemos usar essa mesma fórmula para os outros eixos.
Se é o ângulo que forma com o eixo :
E é o ângulo que forma com o eixo :
Resposta
A intensidade do momento de binário resultante é . Os ângulos diretores são , e .