4.16. O poste de energia elétrica suporta as três linhas. Cada linha exerce uma força vertical sobre o poste devido ao próprio peso, conforme mostra a figura. Determine o momento resultante na base D provocado por todas essas forças. Supondo que seja possível que o vento ou o gelo sejam capazes de romper as linhas, determine qual ou quais linhas, quando rompidas, criariam a condição para o máximo momento em relação à base. Qual será esse momento resultante?
Passo 1
Vamos começar esquematizando o problema
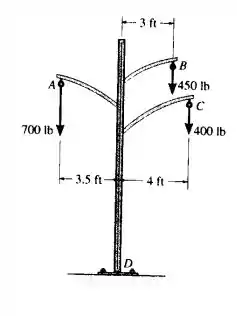
Lembrando que o momento total é a soma de todos os momentos
Passo 2
Precisamos determinar o momento que o peso em cada linha exerce no ponto D e depois somar tudo. Mas as contas vão ficar mais fáceis, porque todas as forças estão paralelas ao poste, então temos
Podemos deixar o sinal positivo se mudarmos nosso referencial, quero dizer
Girando no sentido horário.
Passo 3
O exercício também pede pra gente determinar qual linha cortada vai gerar o momento máximo, ora, basta analisar os sinais da equação, repare que o momento em A é oposto aos momentos em B e C, isso podemos ver até pelo desenho, então, se o cabo A for cortado teremos o momento máximo
Ou
No sentido horário.
Resposta
Quando cortarmos o cabo A teremos o momento maximizado, para esse caso
Todos os momentos estão nos sentido horário.