Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 81b
Resolver o Prob 4.80, considerando a viga do Prob 4.77
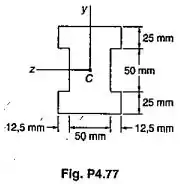
Passo 1
Para determinar o fator de forma, precisamos calcular o momento elástico da viga. (Para mais detalhes, veja a questão 4.78a)
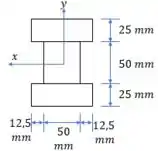
O momento elástico é o maior momento que a viga pode aguentar sem entrar em escoamento.
Então calculamos as propriedades geométricas
E com isso calculamos o momento para a maior tensão possível:
Passo 2
A gente já tem o valor de e de , então o fator de forma pode ser calculado:
Resposta
Exercícios de Livros Relacionados
Cinco tiras de metal, cada uma com 40 mm de largura, são firmemente unidas, de maneira a formar a viga composta mostrada. Os módulos de elasticidade são de 210G P a para o aço, 150G P a para o latão e
Cinco tiras de metal, cada uma com 40 mm de largura, são firmemente unidas, de maneira a formar a viga composta mostrada. Os módulos de elasticidade são de 210G P a para o aço, 150G P a para o latão e
Cinco tiras de metal, cada uma com 40 mm de largura, são firmemente unidas, de maneira a formar a viga composta mostrada. Os módulos de elasticidade são de 210G P a para o aço, 150G P a para o latão e
Um tubo de aço e um de alumínio são firmemente unidos para formar a viga composta mostrada. Os módulos de elasticidade valem 200G P a para o aço e 70G P a para o alumínio. Para um momento fletor de 1,
Um tubo de aço e um de alumínio são firmemente unidos para formar a viga composta mostrada. Os módulos de elasticidade valem 200G P a para o aço e 70G P a para o alumínio. Para um momento fletor de 1,