Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 129

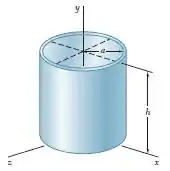
Sabendo que a casca cilíndrica delgada mostrada na figura tem massa m , espessura t e altura h , determine o momento de inércia de massa da casca em relação ao eixo x : (Dica: Considere que a casca é formada removendo-se um cilindro de raio a e altura h de um cilindro de raio a + t   e altura h ; despreze os termos contendo t 2 e t 3 , e mantenha aqueles termos que contenham t .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Pela equação do momento de inércia de um cilindro sólido, temos:

I x = 1 12 m 3 a 2 + h 2 + m h 2 2

I x = 1 12 m 3 a 2 + 4 h 2

Passo 2

O exercício já nos diz qual procedimento tomar. Vamos fazer a subtração do cilindro interno pelo externo. Sendo assim:

I = I e x t - I i n t

I = 1 12 m 1 3 a + t 2 + 4 h 2 - 1 12 m 2 3 a 2 + 4 h 2

Passo 3

Considerando o sólido como um corpo de massa uniforme, podemos considerar a massa em função da densidade e do volume:

m = ρ V

m 1 = ρ π a + t 2 h

m 2 = ρ π a 2 h

Passo 4

Substituindo na equação da inércia, temos:

I x = 1 12 ρ π a + t 2 h 3 a + t 2 + 4 h 2 - 1 12 ρ π a 2 h 3 a 2 + 4 h 2

Expandindo as componentes a + t 2 e desprezando as componentes t 2 e t 3 , temos que:

I x = ρ π h a t 12 12 a 2 + 8 h 2

I x = 4 m 24 3 a 2 + 2 h 2

Resposta

I x = 4 m 24 3 a 2 + 2 h 2

Ver Outros Exercícios desse livro