Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 154

Uma seção de chapa de aço de 2 m m   de espessura é cortada e dobrada para formar o componente de máquina mostrado na figura. Sabendo que a massa específica do aço é 7850 k g / m 3 , determine os produtos de inércia I x y , I y z   e   I z x do componente.

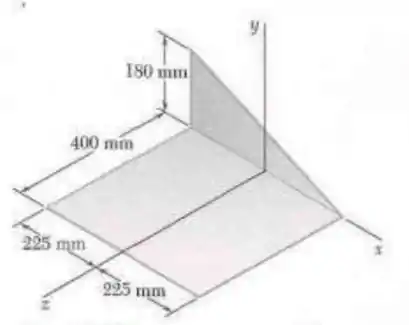
Passo 1

Primeiramente vamos dividir nossa seção de chapa em duas chapas: uma que tá na horizontal e uma em pé. Calculemos, então, a massa de cada componente fazendo

m = ρ a ç o ⋅ V

m 1 = 7850 ⋅ 0.002 ⋅ 0.4 ⋅ 0.45 = 2.826 k g

m 2 = 7850 ⋅ 0.002 ⋅ 1 2 ⋅ 0.45 ⋅ 0.18 = 0.63585   k g

Conseguimos inferir da análise da imagem que

I x ' y ' 1 = I y ' z ' 1 = I z ' x ' 1 = I y ' z ' 2 = I z ' x ' 2 = 0

Então ficamos apenas com

I x ' y ' 2 , a r e a = - 1 72 ⋅ b 2 2 ⋅ h 2 2

Sendo assim, temos

I x ' y ' 2 = ρ a ç o ⋅ V = ρ a ç o ⋅ t ⋅ I x ' y ' 2 , a r e a = ρ a ç o ⋅ t ⋅ - 1 72 ⋅ b 2 2 ⋅ h 2 2 = - 1 36 ⋅ m 2 b 2 h 2

E ainda

x 1 - = y 1 - = z 2 - = 0  

x 2 - = - 0.225 + 0.45 3 m = - 0.075 m

Passo 2

Finalmente podemos calcular os momentos de inércia que serão dados por

I x y = ∑ I x y - + m ⋅ x - ⋅ y - = 0 + 0 + - 1 36 ⋅ 0.63585 ⋅ 00.45 ⋅ 0.18 + 0.63585 ⋅ - 0.075 ⋅ 0.18 3

I x y = - 4.29 ⋅ 10 - 3   k g ⋅ m 2

Por fim, para I y z e I z x temos que seus valores serão iguais a zero devido ao fato de cada componente envolvido no somatório ser igual a zero.

Resposta

I x y = - 4.29 ⋅ 10 - 3   k g ⋅ m 2

I y z = 0

I z x = 0

Ver Outros Exercícios desse livro