Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 156

Uma seção de chapa de aço de 2 mm de espessura é cortada e dobrada para formar o componente de máquina mostrado na figura. Sabendo que a massa específica do aço é 7.850 kg/m³, determine os produtos de inércia I x y , I y z e I z x   do componente.

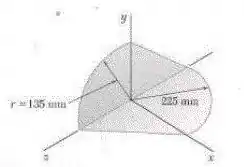
Passo 1

Antes vamos separar cada componente, de tal modo que:

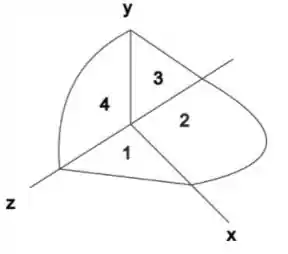
Passo 2

Agora, que separamos cada parte, vamos computar a massa de cada componente. Desse modo, sabemos que:

m = ρ e A

Então,

m 1 = m 3 = 7850 * 0.002 * 1 2 * 0.225 * 0.135 = 0.23844   k g

m 2 = 7850 * 0.002 * π 4 * 0.225 2 = 0.62424   k g

m 4 = 7850 * 0.002 * π 4 * 0.135 2 = 0 . 22473   k g

Passo 3

Certo! Estamos quase terminando! Mas antes, observe que por causa da simetria os produtos centroides da inércia de cada componente são zero.

Além disso, temos:

y - 1 =   y - 2 = 0

x - 3 =   x - 4 = 0

Sabemos que:

I x y = ∑ ( I x ' y ' + m x - y - )

Logo,

I x y = 0

Passo 4

Utilizando os resultados do problema 9.6, caso não tenha respondido da uma conferida e volta para continuarmos, nós temos:

I u v , a r e a   = 1 24 b 2 h 2

Então,

I u v , m a s s a = ρ S T e I u v , a r e a  

= ρ S T e 1 24 b 2 h 2

= 1 12 m b h

Logo,

I z x 1 = 1 12 m 1 b 1 h 1

Enquanto,

I y z 3 = - 1 12 m 3 b 3 h 3

Devido a rotação de 90° dos eixos coordenados.

Passo 5

Vamos guardar as informações que já conseguimos, agora vamos determinar I u v para um quarto de círculo, nós temos

d I u v = d I u ' v ' + u E L v E L d m

Onde,

u E L = u

v E L = 1 2 v = 1 2 a 2 - u 2

Logo,

d m = ρ S T e d A = ρ S T e v d u = ρ S T e a 2 - u 2 d u

Lembre-se que:

I u v = ∫ d I u v = ∫ 0 a u 1 2 a 2 - u 2 ρ S T e a 2 - u 2 d u

= 1 2 ρ S T e ∫ 0 a u a 2 - u 2 d u

= 1 2 ρ e 1 2 a 2 u 2 - 1 4 u 4 a 0 = 1 8 ρ S T e a 4 = 1 2 π m a 4

Portanto,

I z x 2 = - 1 2 m 2 a 2 2

Por causa da rotação de 90° dos eixos coordenados. Como também,

I y z 4 = 1 2 π m 4 a 4 2

Passo 6

Finalmente, com as informações obtidas podemos calcular os produtos de inércia.

Assim,

I y z = ∑ I y z = I y ' z ' + m 1 y 1 - z 1 - + I y ' z ' + m 2 y 2 - z 2 - + I y z 3 + I y z 4

= - 1 12 * 0.23844 * 0.225 * 0.0135 + 1 2 π * 0.22473 * 0.135 2  

I y z = 48.3 * 10 - 6   k g * m 2

E por último,

I z x = ∑ I z x = I z x 1 + I z x 2 + I z ' x ' + m 3 z 3 - x 3 -   + I z ' x ' + m 4 z 4 - x 4 -  

= 1 12 * 0.23488 * 0.225 * 0.135   + - 1 2 π * 0.62424 * 0.225 2

I z x = - 4.43 * 10 - 3 k g * m 2

Resposta

I x y = 0   k g * m 2

I y z = 48.3 * 10 - 6 k g * m 2

I z x = - 4.43 * 10 - 3 k g * m 2

Ver Outros Exercícios desse livro