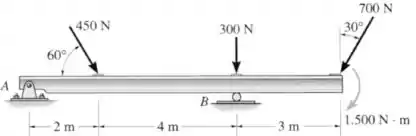
Substitua as cargas atuantes na viga por uma única força resultante. Especifique em que ponto a força atua sobre a viga, tomando como referência a extremidade .
Passo 1
Vamos começar escrevendo cada uma das forças do desenho em forma vetorial, começando da esquerda para a direita:
E então a força resultante é:
Passo 2
E podemos definir esse vetor usando sua intensidade e um ângulo:
E como as duas componentes do vetor são negativas, vamos tomar como referência o ângulo que ele forma com o semieixo horizontal negativo:
Passo 3
Agora vamos calcular o momento resultante dessas três forças em relação ao ponto .
Para fazer isso temos que multiplicar o módulo de cada uma delas pela sua distância perpendicular até o ponto , colocando um sinal negativo nas forças que favorecem a rotação no sentido horário.
Onde o último termo se deve ao momento de que está representado na imagem, apontando no sentido horário.
Nesse caso, apenas as componentes verticais de cada força vão produzir momento, já que as componentes horizontais apontam na direçao do ponto :
Passo 4
Se nós queremos substituir essas três forças por uma única força , ela terá que produzir esse mesmo momento .
Como estamos calculando o momento em relação ao ponto , e a força será aplicada ao longo do elemento , só a componente vertical da força vai produzir momento, ou seja:
E o sinal negativo aparece porque a força deve favorecer a rotação no sentido horário.
Resposta
O sistema pode ser substituído por uma única força a do semieixo horizontal negativo, localizada a m do ponto , ao longo da barra .