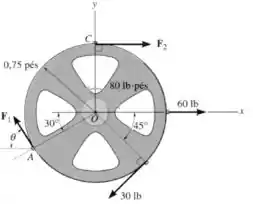
Determine as intensidades de e e a direção e sentido de de forma que as cargas da figura produzam uma força e um momento resultante nulos sobre a roda.
Passo 1
Vamos começar pensando no equilíbrio das quatro forças que agem sobre a roda:
Vamos começar escrevendo e , que são forças conhecidas:
E para as forças e temos que incluir algumas variáveis desconhecidas:
Agora podemos substituir tudo isso na primeira equação:
Para que o vetor resultante seja nulo, todas as componentes precisam se anular, então podemos escrever duas equações a partir daqui:
Por enquanto temos três variáveis (, e ), mas apenas duas equações.
Passo 2
Para encontrar nossa terceira equação, vamos considerar o equilíbrio dos momentos:
Onde estamos calculando os momentos em relação ao ponto .
A força de tem momento nulo, porque sua distância perpendicular até o ponto é nula.
A força de e são tangentes à superfície da roda, então para calcular os seus momentos só precisamos multiplicar seu módulos pelo raio:
Ambos com sinal negativo porque favorecem o sentido horário.
Temos também um binário de módulo no sentido anti-horário. Então por enquanto ficamos com:
Passo 3
E, finalmente, a força não é exatamente tangente à superfície, por isso a expressão para o seu momento é um pouco mais complicada.
Primeiro decompomos a força em duas outras, com módulos e :
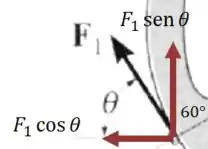
E para calcular o momento de cada uma dessas duas forças em vermelho, só precisamos das suas componentes na direção tangente à roda:
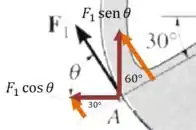
Então:
Então nossa equação de equilíbrio dos momentos fica da seguinte forma:
Vamos simplificar um pouco:
Passo 4
Beleza, agora temos a equaçlão que faltava para completar o sistema:
Vamos multiplicar a primeira equação por , e a segunda por , e então somar tudo:
Vamos substituir esse resultado no sistema original:
Agora vamos dividir a segunda equação pela primeira:
E agora vamos substituir isso em uma das duas primeira equações:
Resposta
As intensidades das forças devem ser e . A força forma um ângulo com o semi-eixo negativo, no sentido horário.