Substitua as cargas sobre a estrutura por uma única força resultante. Especifique onde sua linha de ação intercepta o elemento , tomando como referência o ponto .
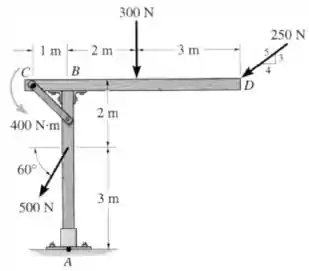
Passo 1
Falaiii meus amores, cêis tão suave?
“Se alguma coisa está dificil de ser feita, é porque não é para ser feita" # sóquenão”

Vamos começar escrevendo cada uma das forças no desenho em forma vetorial, começando da esquerda para a direita:
E então a força resultante é:
E então o módulo da força é:
E o ângulo que ela forma com o semieixo horizontal negativo é:
Para evntuais calculos, temos
Passo 2
Agora vamos calcualr o momento total sobre o sistema em relação ao ponto .
Para isso vamos multiplicar cada força (ou cada componente de força) pela sua distância perpendicular até o ponto , deixando um sinal negativo para as forças que favorecem o sentido horário, e vice-versa.
O momento da força de é:
O da força de é:
O da força de é:
E além disso temos o momento de que está representado no desenho, então:
Passo 3
Quando substituirmos todas essas forças pela força que calculamos no primeiro passo, queremos que o momento em relação ao ponto continue igual, então:
Se formos calcular o momento dessa força resultante no ponto em que a sua linha de ação cruza AB, somente a a componente horizontal fará momento. Considerando que esse ponto esteja a uma altura y, o momento da força resultante é:
Certo, cérebro, eu não gosto de você e nem você de mim, então faça tudo certo pelo menos uma vez para que eu possa continuar te matando com estudos, certo?

Resposta
O sistema pode ser substituído por uma força de formando um ângulo de com o semieixo horizontal negativo, agindo a uma distância de acima do ponto C.